Link-Cut-Tree for Beginners

前言

（我尽量做到不 DFS 式写博客）（
Link-Cut Tree，动态树的一种，似乎没有通用的中文译名。
实现十分容易，没有所谓的那么复杂，基本操作正常码风约 $90$ 行即可完成。
LCT 解决的是什么问题？

【Brainless Version】

Q：给定一棵树，实现单点加，单点求值。
A：其实和树没有关系，本质上是语法题。
Tip：您需至少已经掌握了基本 C++ 语法。

【Easy Version】

Q：给定一棵树，无修改，子树求和。
A：同一棵子树内节点 DFN 序连续，于是把树拍成 DFN，前缀和即可。
Tip：一个点的 DFN 序即对树进行 DFS 时该点被第几个访问。

【Simple Version】

Q：给定一棵树，无修改，链求和。
A：倍增计算 LCA，然后树上差分。
Tip：如果您真的是一名普及组选手，请跳过该版本，本文可以使得您用 LCT 解决 LCA 问题。

【Basic Version】

Q：给定一棵树，子树加，子树求和。
A：在 DFN 上树状数组。
Tip：如果您真的是一名普及组选手，请跳过该版本。

【Normal Version】

Q：给定一棵树，实现换根，子树求和。
A：发现换根是假的，分类讨论后与 Easy Version 相差不大。
Tip：用 Euler Tour Tree 也可以实现。

【Severe Version】

Q：给定一棵树，链加，链求和，子树加，子树求和。
A：树链剖分后线段树维护。
Tip：如果您真的是一名普及组选手，请跳过该版本，本文可以使得您用 LCT 代替树链剖分。

【Hard Version】

Q：给定一棵树，链加，链求和，（换根），断边，加边（保证原结构始终是森林）。
A：LCT 模板。
Tip：本文将会介绍。

接下来，正文开始。

第零部分：约定

1. 朴素的 LCT 是难以解决子树问题的，因此理论上无需维护树上的父子关系，但是我们假定树仍然是有根树。
2. 本质上来说 LCT 维护的是森林而不是树。
3. 下文代码中：fa[x] 为 $x$ 的父节点，ch[x][0] 为 $x$ 的左儿子，ch[x][1] 是右儿子，get(x) 即为判断 $x$ 是其父节点的左儿子（返回 $0$）还是右儿子（返回 $1$）。

第一部分：AuxTree (辅助树)

实链剖分

您并不需要重链剖分的前置知识。
我们人为地钦定树上的点的某一个儿子是实儿子，其他儿子是虚儿子。
然后，定义一个点与它实儿子之间的边为实边，其他边为虚边。
若干个实边首尾相接便形成一条实链。
注意，每一个虚叶子节点也算作一条实链。
此时，原树就被划分成若干条实链，用虚边进行连接。
性质：实链一定是从头到尾自上而下的，也就是说，实链不存在“拐点”。
该结论反证是容易的。

辅助树

（再次强调，假设原树是有根树！）
本质上是一个辅助森林。
我们已经把树“切割”成了若干条实链。
在原树上，实链是一条链；在辅助树上，每一条实链就都变成了一棵树。
也就是说，辅助树就是把原树的实链拿出来爆改，然后再用虚边把这些爆改过的实链联通，当然，每个节点是不会改变的，也就是说辅助树只是对原树进行重新连边。
我们管被爆改过的实链叫做 “实树”（自己起的名字，轻喷）。
爆改实链也不能乱改，实链改完形成的“实树”必须是棵 Splay（不认识没关系，后面会说，现在你只需知道它是一棵二叉树），而且它的中序遍历必须是原树中从上到下遍历的顺序。
用虚边联通当然也不能乱连，原树中哪些“实链对“被虚边连接，辅助树上这对“实树”也要被虚边所连接。
当然，具体把两棵“实树”上哪两个点连在一起，这也是不能随意的，原来两条实链之间的虚边的上下关系不能变。
也就是说，原来这条虚边上面连着实链 A 中的点，下面连着实链 B 中的点，那么在辅助树中，这条虚边也必须要上面连着“实树” A 中的点，下面连着“实树” B 中的点。
还有就是，只有“实树”的根有权利向上连，并且这个根（设为 $r$）向上与 $v$ 连去的那条虚边唯一对应着该棵实树中序遍历的第一个点 $u$ 在原树中与 $v$ 相连的虚边。
听着很绕，实际上很好懂。
画个图举例：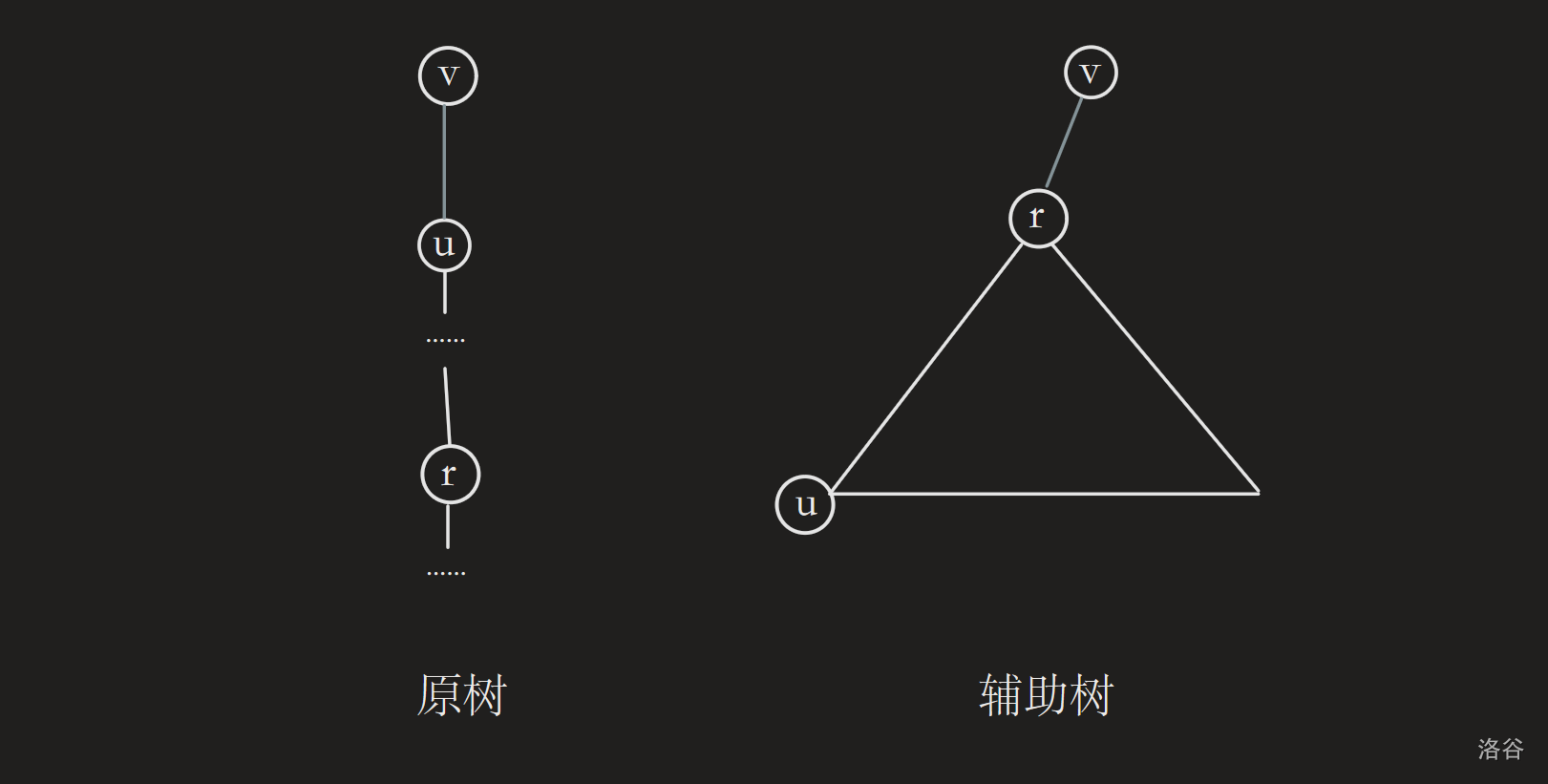

灰色的虚边在原树和辅助树中的位置即如上图所示。
因此，原树和辅助树的虚边之间可以一一对应，并且任意一个辅助树都对应着唯一一棵原树。
还有一点是，辅助树的虚边是认父不认子的，以上图举例，辅助树中 $fa_r=v$，但是 $son_v=\text{null}$，只有“实树”内部的边才是双向的。
同时，虚边上面连的点在原树和辅助树中都是一样的，但是下方不一定。

我们来具体举一个例子。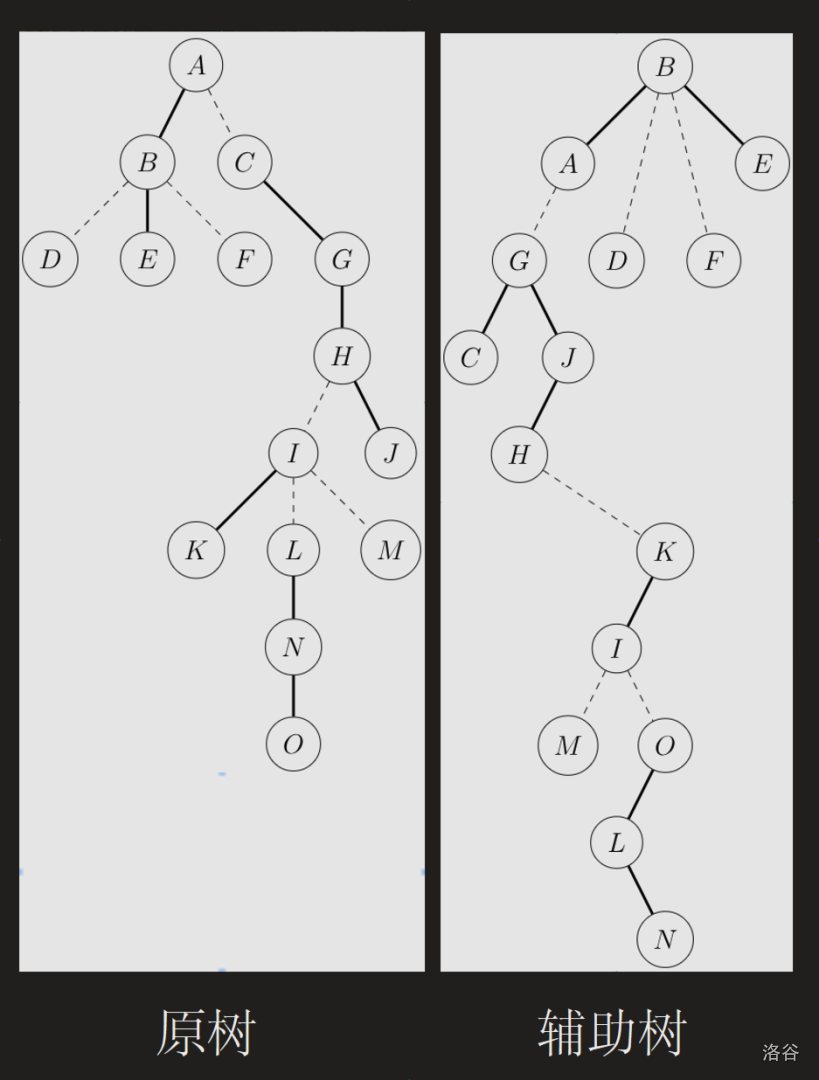

您可以自己手造一些原树然后构造其辅助树以加深理解。
辅助树衍生了一些基本操作：

1. 判断节点是否为某一棵“实树”的根 #define isroot(x) (ch[fa[x]][0]!=x&&ch[fa[x]][1]!=x)
2. 判断节点是辅助树上其父亲的左/右儿子 bool get(int x){return (x==ch[fa[x]][1]);}
3. 整合左右儿子信息用的 void maintain(int x){sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+1;} （此处以子树大小举例）

第二部分：辅助操作

以下操作皆在辅助树上完成。

Splay 树

二叉搜索树是一棵中序遍历为升序的二叉树。
平衡树是一种特殊的二叉搜索树，它的树高被控制在严格 $O(\log n)$ 或均摊 $O(\log n)$。
Splay Tree 是一种典型的树高均摊 $O(\log n)$ 的平衡树。
LCT 所需要的 Splay 与正常的 Splay 有细微差别，正常的 Splay 主要用于维持树的平衡，而此处的 Splay 是为了维护动态树所需要的结构，因此您在未掌握平衡树知识的前提下也可以放心食用。
Splay 树的关键操作是：Splay 操作。（听起来很废话呢）
Splay 操作主要通过旋转来实现，它的效果是将某一个节点旋转到根。
旋转操作分两种：

单旋

分为左旋（zig）和右旋（zag），它们是很对称的。
勉强用文字描述，其实对某个点旋转就是把它的父节点“拽”下来，放到该点的下面去。
具体地，如果一个点 $x$ 是其父节点 $p$ 的左儿子，那么就让 $p$ 成为 $x$ 的右儿子。
原来 $x$ 的右儿子怎么办？
让它成为现在 $p$ 的左儿子即可。
这就是右旋。

左旋就是把上文中的“左”字和“右”字互换即可。

这是 OI-wiki 中的演示图。

可以这么想象：有一个手将 $x$ “拎”了起来，$p$ 因为重力而下垂，掉到下面，顺便“抢”来了 $x$ 的一个子节点。

单旋有一个性质：单选不改变树的中序遍历（注意：此处“中序遍历”指遍历权值）。
这是很显然的。
下面是代码，它将左旋和右旋写进了同一函数中。

inline void rotate(int x){
		int f=fa[x],gf=fa[f],lr=get(x);
		if(!isroot(f)) ch[gf][f==ch[gf][1]]=x;
		ch[f][lr]=ch[x][lr^1];		
		if(ch[x][lr^1]) fa[ch[x][lr^1]]=f;
		ch[x][lr^1]=f;
		fa[f]=x;
		fa[x]=gf;
		maintain(f);
		maintain(x);
}

后面您将会知道，您目前可以认为我们保证不会对一棵“实树”的根进行 rotate，因此被单旋的节点的父节点一定仍在“实树“内部，但是祖父节点有可能和父节点以虚边相连接，所以需要特判 isroot(f)。

双旋

Zig-Zig/Zag-Zag

设 $p=fa_x,g=fa_p$ 当 $x,p,g$ “共线”，即 $x,p$ 同为左儿子或右儿子时，我们应该先转一下 $p$，再转一下 $x$，如此图。

这样我们就可以把 $x$ 转到上面了。
注意到一个性质，两次旋转同为左旋/右旋。
所以就叫做“zig-zig”或“zag-zag”。

Zig-Zag/Zag-Zig

设 $p=fa_x,g=fa_p$ 当 $x,p,g$ “不共线”，即 $x,p$ 一个是左儿子，一个是右儿子时，我们应该转两下 $x$，如此图。
注意到一个性质，两次旋转一次是左旋，一次是右旋。
所以就叫做“zag-zig”或“zig-zag”。

伸展操作（Splay 操作）

通过若干次双旋和零或一次单旋将 $x$ 旋转到根。
为什么最后可能有一次单旋?
因为我们发现，双旋要判断 $x,p,g$ 是否“共线”，但当 $x$ 为根的儿子时，$g$ 不在该棵实树内，所以只需单旋即可。
代码：

void splay(int x){
		rt=x;
		while(!isroot(x)){
				int f=fa[x],g=fa[fa[x]];
				if(!isroot(f)){
						if(get(f)==get(x)) rotate(f);
						else rotate(x);
				}
				rotate(x);
		}
}

这是易于理解的代码，但很丑陋，可以这么写：

void splay(int x){
    for(int f=fa[x];f=fa[x],!isroot(x);rotate(x)) 
        if(!isroot(f)) 
        	  rotate((get(f)==get(x))?f:x);
    rt=x;
}

最好在理解第一个代码后再看第二个代码。

Access 操作

Access，作为名词是通道；(使用或见到的)机会，权利；通路；入径；
作为及物动词是访问，存取(计算机文件)；进入；到达。
怎么说呢，还是比较名副其实的吧。
它的任务很简单，access(x) 表示在原树上找到节点 $x$，然后把从 $x$ 到根的路径改为一条实链，再把与这条实链连接的所有边变成虚边。
通俗的说，你可以认为 access 是把 $x$ 到原树的根“打通”。
那么，这个东西怎么在辅助树中处理呢？
非常简单。

首先，将 $x$ Splay 到其所在实树的根。
然后，根据辅助树的性质，此时 $x$ 的右子树都属于原树上在其下方的点。
这些点与 access 出的那条实链就没有实边相连了，于是在辅助树中果断“切掉“右子树，也就是让 $x$ 的右儿子向它连虚边。
现在 $x$ 和它的父亲 $f$ 之间连的还是虚边，我们就直接打通这条边，让它变为实边，而且要 $x$ 是右儿子。
但是你先别急，人家 $f$ 自己还有实儿子呢，这是不能要的，所以先把 $f$ Splay 到根，然后切掉右子树（也就是在 $f$ 所处的那条实链上在 $f$ 下方的所有点），然后才能把右儿子连为 $x$。
然后，两棵实树就连通了。
对 $f$ 执行同样的操作，一直连到根，就 access 完成了。
例如，对于这颗原树：

我们要将 $N$ 到 $A$ 进行 access，辅助树上的操作就如下图所示。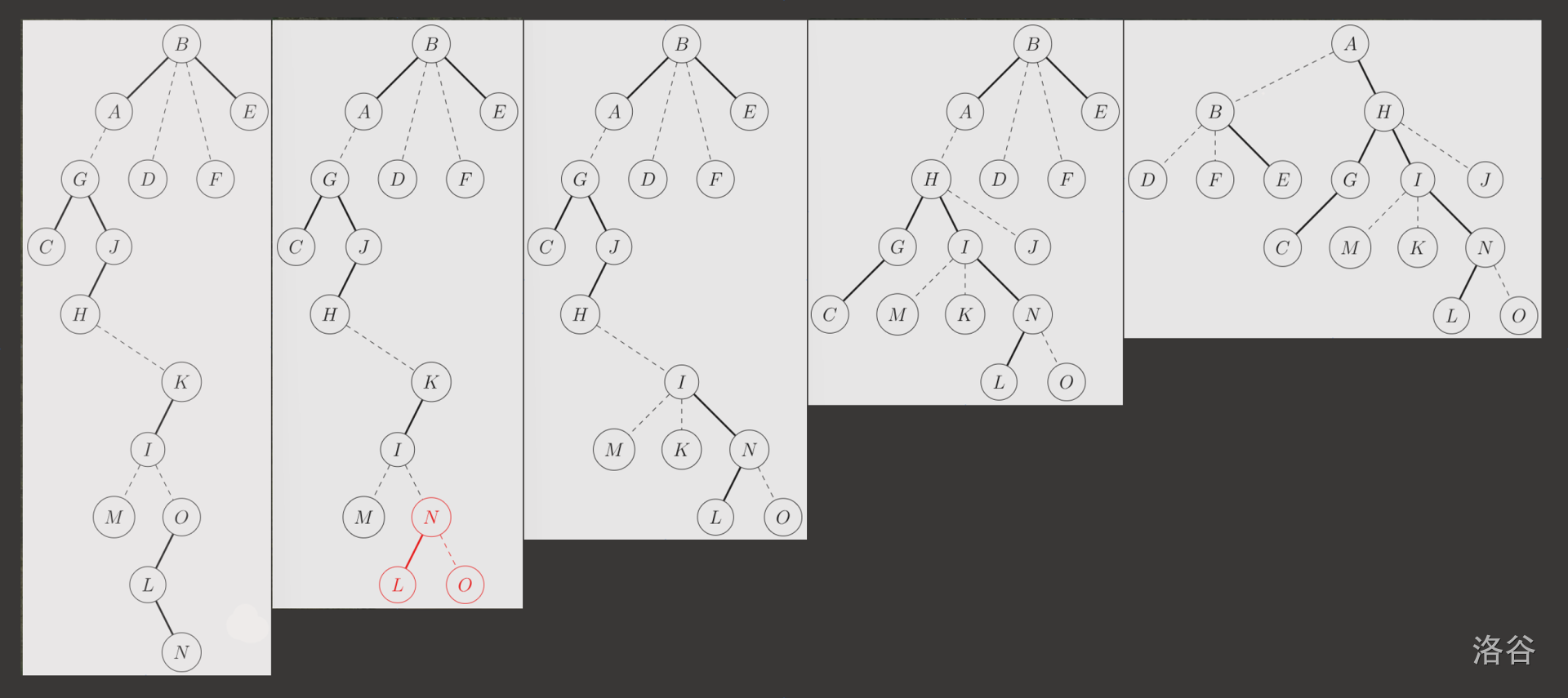

最后原树变成这样：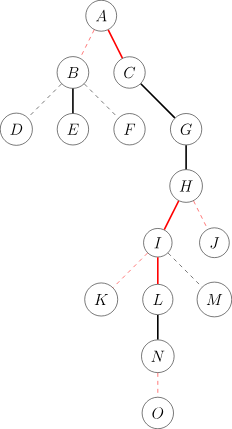

说得复杂，代码很短。

inline int access(int x){
		int p = 0;
		for (p = 0; x; p = x, x = fa[x]){
				splay(x);
				rs(x) = p;
				maintain(x);
		}
		return p;
}

它的返回值是：表示 $x$ 到根的链所在的 Splay 树的根。
返回值的两个性质：

• 这个节点一定已经被旋转到了根节点，且父亲一定为空。
• 连续两次 Access 操作时，第二次 Access 操作的返回值等于这两个节点在原树上的 LCA。

第三部分：反转标记

Makeroot 操作

makeroot(x) 表示把 $x$ 换为原树的根。
我们不妨考虑每个节点的父节点的变化情况。
不难发现，如果节点 $k$ 不在 $x$ 到根的链上，那么其父节点不会变。
链上的父子关系则会全部反转。
反转链上的父子关系，怎么做？
非常容易，首先执行 access(x)，就可以将 $x$ 到根的路径拉成一条独立的实链。
这条实链在辅助树上既是一个独立的 Splay 树。
反转这条链上的父子关系，在 Splay 上的本质就是翻转所有的左右儿子关系。

Pushdown 操作

显然，直接翻转是可以被卡到 $O(n)$ 的。
所以我们需要沿用线段树中的懒惰标记思想。
但是并没有线段树基础其实也是不影响的，懒惰标记的本质实际上是延后处理，也就是说，我们不需要在每次 Makeroot 的时候都对整棵 Splay 进行左右儿子翻转，仅仅需要为 Splay 的根节点 $x$ 打上一个反转标记，然后仅仅 swap 根节点的左右儿子 $ls,rs$，剩下的不用管。
等到下次要用到 $r$ 的时候，将 $x$ 的反转标记下传到 $ls,rs$，然后清空 $r$ 的标记，翻转 $ls,rs$ 的左右儿子。
这就意味着，只有一个节点将要被操作或访问的话，才会下传标记，然后进行翻转，保证了复杂度。
于是，我们有下传标记的代码：

inline void pushdown(int x){
		if (tag[x]){
				if (ls(x)){
						tag[ls(x)] ^= 1;
						swap(ls(ls(x)), rs(ls(x)));
				}
				if (rs(x)){
						tag[rs(x)] ^= 1;
						swap(ls(rs(x)), rs(rs(x)));
				}
				tag[x] = 0;
		}
}

Update 操作

什么时候节点会被操作或访问？
答案就是进行 Splay 操作的时候。
所以我们需要修改 Splay 操作的代码。
我们知道，Splay 操作仅仅涉及 $x$ 到根的节点，所以我们引入 update 操作：对 $x$ 到根的所有节点都执行 Pushdown 操作。
代码十分容易：

void update(int p){
    if (!isroot(p)) update(fa[p]);
    pushdown(p);
}

因此我们有了新的 Splay 操作（仅仅增加了一句 update）：

void splay(int x){
		update(x);
    for(int f=fa[x];f=fa[x],!isroot(x);rotate(x)) 
        if(!isroot(f)) 
        	  rotate((get(f)==get(x))?f:x);
    rt=x;
}

第四部分：主体

Split 操作

我们知道，Access 操作可以把 $x$ 到根的路径拉成一条独立实链。
那么如果我们想要把 $x$ 到 $y$ 的路径拉成独立实链呢？
其实是容易的。
你只需要将 $x$ 变成根，即执行 Makeroot 操作即可。
然后就是正常的对 $y$ 进行 Access 操作。
为了方便以及保证复杂度，我们再对 $y$ 进行 Splay，以使其成为所在实树的根。
所以代码只有简短三行。

inline void split(int x, int y){
		makeroot(x);
		access(y);
		splay(y);
}

Find 操作

find(x) 返回 $x$ 所在原树的根，而不是辅助树。
考虑 Access 操作的返回值：表示 $x$ 到根的链所在的 Splay 树的根。
这棵 Splay 树的根并不是什么关键节点，但是根据辅助树的性质，这棵 Splay 上 DFN 序最小的节点，即“最左“的那个点，在原树上对应着原树的根。
所以 Access 之后从 Splay 的根开始一直往左儿子跑就能找到其所在原树的根了。
跑的过程中要不停的进行 Pushdown 操作以下放标记。

这是可能会有疑问：为什么 Split 的时候没有 Pushdown?
显然因为 Makeroot、Access、Splay 的时候已经 Pushdown 过了。

代码十分容易：

inline int find(int p){
		access(p);
		splay(p);
		pushdown(p);
		while (ls(p)){
				p = ls(p);
				pushdown(p);
		}
		splay(p);
		return p;
}

同样，为了方便以及保证复杂度，最后要进行 Splay 操作。

Link 操作

真正地进入 Link-Cut Tree 的关键环节。

首先，动态树显然是不能有环的，所以在 link(x,y) 的时候，如果 $x,y$ 本身就在同一棵原树上就不能连边。
怎么判断 $x,y$ 是否在同一棵原树上呢？
其实就是判断 find(x)==find(y)。
但是实际上我们不这么做。
而是先 makeroot(x)，然后判断 x==find(y)，如果没有 return 就 splay(x)。
其实两种是等价的，但是后者可以使得 $x$ 同时变为其所在原树和实树的根。
这么做的原因也很简单，因为这样以后 Link 就变得十分方便了，直接让 fa[x]=y，即连一条认父不认子的虚边，完事（因为只有同时作为原树和实树的根节点才有权利向上连虚边）。

inline void link(int x, int y){
		makeroot(x);
		if (x == find(y)) return;
		splay(x);
		fa[x] = y;
}

Cut 操作

显然如果本身 $x,y$ 之间就没有边，那么 cut(x,y) 是没用的。
怎么判断 $x,y$ 是否在原树上是否直接连边呢？
首先如果它们都不在同一原树上，那想都不用想，肯定没有连边，直接 return。
否则我们继续走，先 split(x,y)，把 $x$ 到 $y$ 的路径拿出来做一条独立实链。
注意，根据 Split 操作的性质，此时 $x$ 是原树的根，但是 $y$ 是实树的根。
也就是说 $x$ 在原树上肯定比 $y$ 深度浅，所以在实树上 $x$ 肯定在 $y$ 的左子树内。
如果 $x,y$ 之间有直接连边，那么 Split 之后它们所在的实树不可能还有其他节点，因此 $x$ 肯定在 $y$ 的左子树内这条性质可以强化为 $x$ 就是 $y$ 的左儿子。
但是你只判 x==ls(y) 肯定会出锅，如果 $x,y$ 之间在原树上有连边，那么 $x$ 的右子树肯定是空，要不然原树上 $y$ 的父亲就不可能是 $x$，肯定是 $x$ 右子树中最右的节点。
因此还需要判断 rs(x)==0。
也就是说，split(x,y) 之后只要有 x==ls(y)&&!rx(x) 就能保证 $x,y$ 在原树上有直接连边。
然后直接断开就行，也就是令 ls(y)=0,fa[x]=0。
注意，执行 fa[x]=0 是必要的，应为此时我们是在原树上彻底断边，而不是断实边为虚边。
在最后进行 maintain(y) 以更新。
代码也极其容易。

inline void cut(int x, int y){
		if (find(x) != find(y)) return;
		split(x, y);
		if (ls(y) == x && !rs(x)){
				ls(y) = fa[x] = 0;
				maintain(y);
		}
}

完整代码

#include <bits/stdc++.h>
#define sor(i, l, r) for (int i = l; i <= r; i++)
#define int long long
using namespace std;
const int N = 5e5;
namespace Revitalize
{

    //130 without ya hang
    class Link_Cut_Tree{
    public:
        int a[N], sz[N], ch[N][2], tot, fa[N], val[N], root, tag[N];
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
#define isroot(x) (ch[fa[x]][0] != x && ch[fa[x]][1] != x)
        inline void maintain(int x){sz[x] = sz[ch[x][0]] ^ sz[ch[x][1]] ^ val[x];}
        inline void pushdown(int x){
            if (tag[x]){
                if (ls(x)){
                    tag[ls(x)] ^= 1;
                    swap(ls(ls(x)), rs(ls(x)));
                }
                if (rs(x)){
                    tag[rs(x)] ^= 1;
                    swap(ls(rs(x)), rs(rs(x)));
                }
                tag[x] = 0;
            }
        }
        bool get(int x){return (x == ch[fa[x]][1]);}
        inline void rotate(int x){
            int f = fa[x], gf = fa[f], lr = get(x);
            if (!isroot(f)) ch[gf][ch[gf][1] == f] = x;
            ch[f][lr] = ch[x][lr ^ 1];
            fa[ch[x][lr ^ 1]] = f;
            ch[x][lr ^ 1] = f;
            fa[f] = x;
            fa[x] = gf;
            maintain(f);
            maintain(x);
        }
        void update(int p){
            if (!isroot(p)) update(fa[p]);
            pushdown(p);
        }
        inline void splay(int x){
            update(x);
            for (int f; f = fa[x], !isroot(x); rotate(x)) if (!isroot(f)) rotate((get(f) == get(x)) ? f : x);
        }
        inline int access(int x){
            int p = 0;
            for (p = 0; x; p = x, x = fa[x]){
                splay(x);
                rs(x) = p;
                maintain(x);
            }
            return p;
        }
        inline void makeroot(int x){
            x = access(x);
            swap(ls(x), rs(x));
            tag[x] ^= 1;
        }
    public:
        inline int find(int p){
            access(p);
            splay(p);
            pushdown(p);
            while (ls(p)){
                p = ls(p);
                pushdown(p);
            }
            splay(p);
            return p;
        }
        inline void link(int x, int y){
            makeroot(x);
            if (x == find(y)) return;
            splay(x);
            fa[x] = y;
        }
        inline void split(int x, int y){
            makeroot(x);
            access(y);
            splay(y);
        }
        inline void cut(int x, int y){
            if (find(x) != find(y)) return;
            split(x,y);
            
            if (ls(y) == x && !rs(x)){
                ls(y) = fa[x] = 0;
                maintain(y);
            }
        }
    } tr;
    int n, m;

    inline void work()
    {
        cin >> n >> m;
        for (int i = 1; i <= n; i++)
        {
            cin >> tr.val[i];
            tr.sz[i] = tr.val[i];
        }
        for(int i=1;i<=n;i++)
        {
            tr.find(i);
        }
        while (m--)
        {
            int op;
            cin >> op;
            if (op == 0)
            {
                int u, v;
                cin >> u >> v;
                tr.split(u, v);
                cout << tr.sz[v] << "\n";
            }
            if (op == 1)
            {
                int u, v;
                cin >> u >> v;
                tr.link(u, v);
            }
            if (op == 2)
            {
                int u, v;
                cin >> u >> v;
                tr.cut(u, v);
            }
            if (op == 3)
            {
                int u, v;
                cin >> u >> v;
                tr.splay(u);
                tr.val[u] = v;
                tr.maintain(u);
            }
        }
    }
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    return Revitalize::work(), 0;
}

常数比较小，可以通过模板。